1x1 der Statistik: Das Problem mit dem p-Wert • Wissen Was Wirkt

Der p-Wert ist in der Forschung allgegenwärtig – jeder kennt ihn, viele nutzen ihn, doch kaum jemand kann seine Bedeutung erklären. Er wird oft für Aussagen herangezogen, für die er nicht gedacht ist.

Der p-Wert ist einer der bekanntesten statistischen Werte. Er wird in Studien oft für die Bewertung herangezogen, ob ein Effekt vorliegt oder nicht. Doch dafür ist p nicht gedacht. Anhand von den Arbeiten wichtiger Statistiker*innen erklären wir Ihnen heute die Probleme der statistischen Signifikanz genauer.

Was ist überhaupt der p-Wert? Eine Veranschaulichung

Dein Freund übt Münzwürfe und will dir versichern, dass die Münze fair ist (Nullhypothese: Wahrscheinlichkeit Kopf zu erhalten liegt bei 50%). Du bist etwas skeptisch und beobachtest ihn erst einmal. Dir fällt auf, dass in 9 von 10 Würfen Kopf herauskommt (beobachtete Wahrscheinlichkeit 90% für Kopf). Doch jetzt weißt du nicht ob das nur Zufall war, oder ob die Münze wirklich gezinkt ist. Du überlegst dir, wie wahrscheinlich das beobachtete Ergebnis ist, wenn die Münze tatsächlich fair ist (der p-Wert unter der Nullhypothese). Je kleiner p ist, desto weniger wahrscheinlich ist es 9 von 10 Kopf-Würfen zu erhalten, wenn die Münze fair ist.

Für die Interessierten: Eine Definition

Unter der Annahme, dass der “wahre“ nicht beobachtbare Effekt reiner Zufall ist (also die Nullhypothese zutrifft) gibt p die Wahrscheinlichkeit dafür an, dass der wahre Wert mindestens so groß ist wie das erhaltene Ergebnis in der aktuellen Studie. Der p-Wert misst also die Inkompatibilität von Nullhypothese und Daten [1]. Je kleiner p, desto inkompatibler sind die gefunden Daten mit der Zufallsannahme. P kann also für Zweifel an der Nullhypothese herangezogen werden.

Was der p-Wert nicht aussagt!

Der p-Wert gibt keine Information darüber, wie wahrscheinlich es ist, dass die untersuchte Hypothese wahr ist. Vielleicht haben Sie schon einmal gehört, dass die Hypothese bestätigt wurde, weil das Ergebnis statistisch signifikant war. Das ist keine korrekte Interpretation von p. Er misst nicht die Wahrscheinlichkeit, dass die untersuchte Hypothese wahr ist oder dass die Daten nur durch Zufall entstanden sind [1]. Der p-Wert beschreibt, wie gut die Daten mit der Nullhypothese übereinstimmen. Wie passend die Hypothese ist, ist eine inhaltliche Frage.

Wofür p-Wert nicht genutzt werden sollte

Der p-Wert ermöglicht keine Aussagen über die Wichtigkeit oder die Größe eines Effekts, denn er hängt stark von der Größe der Stichprobe ab[1].
Bei großen Stichproben kann selbst ein minimaler Effekt statistisch signifikant sein, während bei kleinen Stichproben auch große Effekte möglicherweise nicht signifikant werden. Der gleiche geschätzte Effekt hat also abhängig von der Stichprobengröße einen anderen p-Wert!

Das Problem mit der statistischen Signifikanz

Meist wird p < 0.05 als Schwellenwert für die statistische Signifikanz verwendet. Diese willkürlich festgelegte Grenze führt oft dazu, dass Ergebnisse mit p > 0.05 (nicht signifikante Ergebnisse) in der Größe und Wichtigkeit heruntergespielt werden, während Ergebnisse mit p < 0.05 (signifikante Ergebnisse) tendenziell überschätzt und häufiger berichtet werden [2]. Diese Tendenz, nur Studien zu veröffentlichen oder hervorzuheben, die statistisch signifikante Ergebnisse liefern, führt zu einer selektiven Berichterstattung. Diese ist ein großes Problem für den wissenschaftlichen Diskurs, weil auch statistisch nicht signifikante Studienergebnisse wichtige Informationen beinhalten. Die Präregistrierung von klinischen Studien ist ein wichtiges Mittel, um dieser Verzerrung entgegenzuwirken [3].

Nicht signifikant heißt nicht gleich kein Effekt

Wer nur auf die statistische Signifikanz schaut, denkt vielleicht: Wenn p über 0.05 liegt gibt es keinen Effekt. Das führt dazu, dass man Effekte und Unterschiede verkennt, die einem Laien direkt auffallen würden, wenn er sich die Verteilung der Ergebnisse z.B. im Konfidenzintervall oder in einer Verteilungskurve anschaut [2].

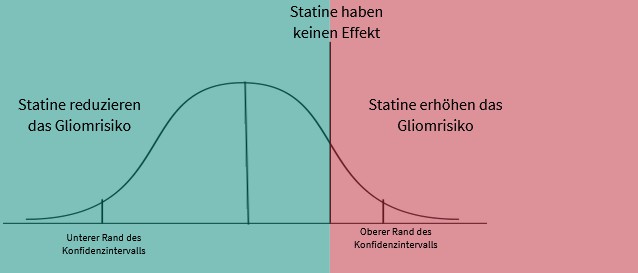
Matthews (2021) nennt als Beispiel die Rolle von Statinen bei der Risikoreduktion für bestimmte Hirntumore, sogenannte Gliome. Eine große Studie aus dem Jahr 2016 fand eine Risikoreduktion von etwa 25%, was die bisherige Theorie „Statine können Gliome reduzieren“ bestätigte. Es gab nur ein Problem: Das Unsicherheitsintervall (95% Konfidenzintervall) reichte von einer Reduktion um 52% bis hin zu einer Erhöhung des Risikos um 17% (siehe Abbildung oben). Der p-Wert betrug 0,2, was als nicht signifikant gilt. Ausgehend vom p-Wert kamen die Forschenden zu dem Schluss: Unsere Studie unterstützt nicht die Theorie, der Risikoreduktion durch Statine . Betrachtet man jedoch die Wahrscheinlichkeitsverteilung, lässt sich eine solche Schlussfolgerung nicht eindeutig ziehen [4].

Nicht signifikant heißt nicht gleich Konflikt

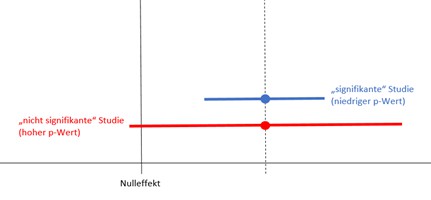
Außerdem sollte man nicht automatisch einen Konflikt zwischen 2 Studien sehen, nur weil eine Studie ein statistisch signifikantes Ergebnis hat, die andere aber nicht [2]. Der geschätzte mittlere Effekt könnte nämlich identisch sein (s. Abbildung unten). Die rote Studie hat zum Beispiel nur aufgrund einer kleineren Stichprobe ein breiteres Konfidenzintervall. Dies schneidet den Nulleffekt und ist damit nicht statistisch signifikant. Die Mehrheit des Konfidenzintervalls würde jedoch für einen Effekt sprechen. Es liegt also kein Konflikt vor, die Ergebnisse der roten Studie sind einfach sehr unpräzise! Es besteht hier die Möglichkeit, dass wir uns beim wahren Wert stärker irren könnten.

p < 0.05 ist keine gute Entscheidungshilfe

P allein ist kein ein gutes Maß für die Beurteilung der Evidenz bezüglich einem Modell oder einer Hypothese [1]. Ohne weitere Informationen ist nicht klar, ob ein anderes Modell die Daten besser erklären könnte. Deshalb sollten wissenschaftliche Schlussfolgerungen und politische oder wirtschaftliche Entscheidungen nie alleine auf p < 0.05 basieren [1]. Hier sind Kontextinformationen wie Studienqualität, die Erfüllung der Modellvorrausetzungen und Studiendesign heranzuziehen.

Sollte man den p-Wert abschaffen?

Bei dieser Frage gehen die Meinungen der Statistiker*innen auseinander [3]. Für manche ist es ausreichend, zusätzliche Informationen wie zum Beispiel die Lage und Breite des Konfidenzintervalls oder die Größe des Effekts für die Interpretation heranzuziehen. Manche lehnen die Verwendung des p-Wertes strikt ab und verweisen auf beispielsweise bayesianische Methoden [z.B. 5] oder entscheidungstheoretische Modellierungen [z.B. 6].
Das Cochrane Handbook [7] rät dazu, auf die Einordnung als statistisch signifikant zu verzichten und stattdessen das 95% Konfidenzintervall gemeinsam mit dem exakten p-Wert zu berichten. P bezeichnet eine kontinuierliche Wahrscheinlichkeit von 0 – 100 und sollte auch so interpretiert werden.