In unserem letzten „Einmaleins der Statistik“ ging es um den p-Wert, der Auskunft über die statistische Signifikanz eines Ergebnisses gibt. Wichtige Zusatzinformationen liefert das Konfidenzintervall (KI), das wir heute in aller Kürze vorstellen.
Jedes statistische Ergebnis ist nur ein Schätzwert, der mehr oder minder dicht am wahren, aber notgedrungen unbekannten Wert liegt. Denn wir können ja in einer Studie nicht ALLE betroffenen Patient*innen untersuchen, sondern immer nur eine Stichprobe, von der wir dann auf die große „Wahrheit“ schließen. Und dabei bleibt immer eine gewisse Unsicherheit bestehen.
Das Konfidenzintervall (KI) hilft uns, diese Rest-Unsicherheit einzuschätzen, indem es einen Vertrauensbereich liefert, in dem der wahre Wert mit hoher Wahrscheinlichkeit liegt. In der Praxis nutzt man dafür das 95%-KI, also den Bereich, in dem das wahre Ergebnis mit 95-prozentiger Sicherheit liegt. Für KIs gilt: Je kleiner, desto besser. Denn je schmaler der Vertrauensbereich des KIs, desto näher kommt das geschätzte Ergebnis dem wahren Wert.
Was bedeutet das in der Praxis?
Stellen wir uns eine Studie vor, die die Wirkung eines neuen Erkältungsmedikaments mit Placebo vergleicht. Sie kommt zum Ergebnis, dass der neue Wirkstoff die Dauer der Erkältung im Durchschnitt von sieben Tagen (bei Einnahme von Placebo) auf fünf Tage reduziert. Das 95%-KI reicht von 3,5 Tagen bis zu 6,5 Tagen. Was bedeutet das?
Der „wahre“ Wert für die Dauer der mit dem neuen Mittel behandelten Erkältung weicht vermutlich geringfügig von fünf Tagen ab. Doch mit 95-prozentiger Sicherheit ist er nicht geringer als dreieinhalb und nicht größer als sechseinhalb Tage. Wichtig in diesem Beispiel: Das Konfidenzintervall schließt den „Nulleffekt“ nicht mit ein, also die sieben Tage eines Schnupfens, der zum Vergleich mit Placebo behandelt wurde. Das bedeutet, dass wir uns ziemlich sicher sein können, dass das neue Medikament tatsächlich eine Wirkung hat. Ziemlich sicher bedeutet ähnlich wie beim p-Wert: Das Restrisiko, daneben zu liegen, ist kleiner als 5 Prozent.
Allerdings ist im KI auch die Möglichkeit enthalten, dass die Erkrankungsdauer durch das Medikament nur um einen halben Tag auf 6,5 verkürzt wird – ein Unterschied, der für Patient*innen kaum relevant sein dürfte. Auch hier muss man also zwischen statistischer Signifikanz und klinischer Relevanz unterscheiden. Wie man statistische Signifikanz und klinische Relevanz am KI erkennen kann, soll die folgende Abbildung deutlich machen:
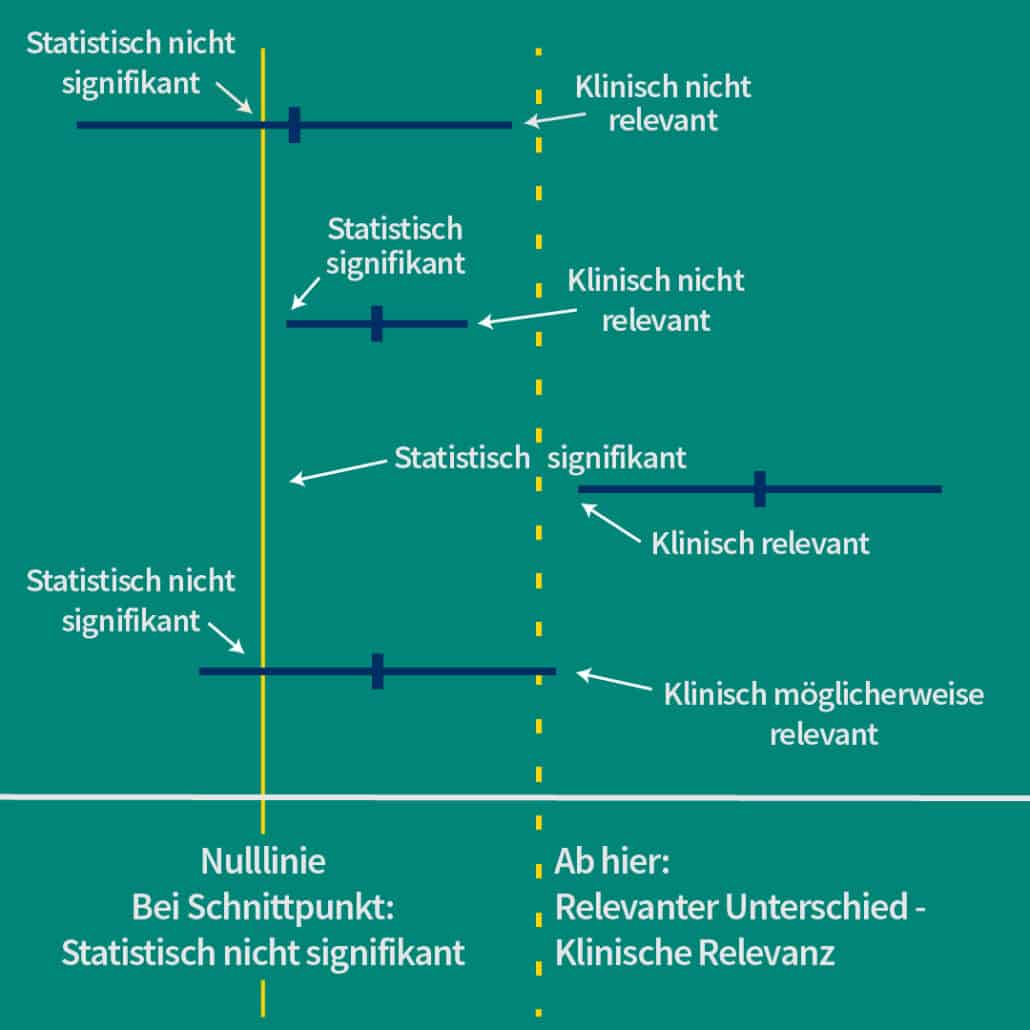
Vier Szenarien für Konfidenzintervalle. Alles rechts von der Nulllinie ( = kein Unterschied zwischen Behandlungs- und Kontrollgruppe) bedeutet ein besseres Abschneiden des Medikaments. Die gestrichelte Linie markiert die nicht minder wichtige Grenze zur klinischen Relevanz. Die Position von Mittelwert und KI in Bezug auf diese Grenzlinien ermöglicht eine schnelle Einschätzung der Ergebnisse.
Schlankheitskur für Konfidenzintervalle
Der Vorteil des KI gegenüber dem p-Wert: Das KI wird in derselben Einheit angegeben wie der Ergebniswert (in unserem Beispiel: Krankheitsdauer in Tagen). Es ist dadurch weniger abstrakt als der p-Wert.
Das unterste Konfidenzintervall in der Abbildung zeigt die Krux großer Konfidenzintervalle: Ihr Effekt ist schwer zu deuten. Eine Möglichkeit, KIs zu verschlanken und damit die Zuverlässigkeit von Ergebnissen zu verbessern, sind mehr Messwerte, sprich: größere Studien mit mehr Studienteilnehmenden. Dem gleichen Zweck dient auch das statistische Zusammenfassen der Ergebnisse mehrerer Studien in einer sogenannten Metaanalyse – doch dazu mehr in einem der nächsten Beiträge aus unserem „Einmaleins der Statistik“.

Text: Dr. Birgit Schindler
Alle Beiträge des „Einmaleins der Statistik“:


