In unserer Serie „Einmaleins der Statistik“ geht es heute um fiese Haifische, leere Gläser und um Risiken, die sich sowohl in absoluten als auch in relativen Zahlen ausdrücken lassen. Beides ist statistisch korrekt. Welchen Eindruck diese Angaben bei Nicht-Statistiker*innen hinterlassen, kann sich jedoch den Unterschied zwischen Hai-Phobie und entspanntem Bad im Meer ausmachen.
„Tödliche Haiangriffe weltweit um 43 Prozent zugenommen!“ So oder ähnlich konnte man es 2013 in den Medien lesen. Das klingt natürlich erst mal ziemlich dramatisch – fast die Hälfte mehr tödliche Angriffe! Die Meldungen basierten auf durchaus vertrauenswürdigen Zahlen des am Florida Museum of Natural History angesiedelten International Shark Attack File (ISAF), das Meldungen über Haiangriffe auf Menschen aus aller Welt sammelt. Also nie wieder im Meer baden?
Das Problem mit der Zahl: Die 43 Prozent beziehen sich auf die relative Veränderung der Zahlen. Schaut man sich die absoluten Zahlen an, die dieser Berechnung zugrunde liegen, dann klingt das Ganze deutlich weniger dramatisch: Während es 2012 weltweit zu sieben tödlichen Haiangriffen kam, waren es 2013 zehn Angriffe, also drei mehr. Vom Ausgangspunkt sieben entspricht ein Anstieg um drei auf zehn tatsächlich 3/7=0,43, also 43 Prozent. Die Angabe des relativen Anstiegs des Risikos ist also nicht falsch. Und trotzdem führt sie schnell in die Irre. Für gute Wissenschaftskommunikation gilt daher die Regel: Vorsicht mit relativen Risiken!
Keine Angst vor Haien und relativen Risiken!
Was hat das Ganze mit Medizin und Studien zu tun? Risiken gehören zu den wichtigsten Kennzahlen in der medizinischen Forschung. Oft begegnen sie uns in Form des relativen Risikos auch bekannt als Risikoverhältnis oder Risk Ratio (RR). Das RR gibt an, wie viel häufiger oder seltener ein bestimmtes Ereignis in einer Gruppe im Vergleich mit einer anderen Gruppe auftritt. Dabei vergleicht man die Raten des Auftretens in beiden Gruppen.

Das Beispiel mit den Haiangriffen hinkt zugegebenermaßen ein bisschen, weil hier die zugrunde liegenden Gruppen nicht klar definiert sind. Um die Zahlen der Haiopfer bewerten zu können, müsste man wissen, wie viele Menschen weltweit in den Jahren 2012 und 2013 im Meer gebadet haben. Und das kann man bestenfalls über den Daumen peilen – unordentliche „Real-World-Daten“ eben.
Wir wollen uns deshalb das fiktive Beispiel einer nach allen Regeln der Kunst randomisierten kontrollierten Studie zu einem Medikament anschauen, das vor Herzinfarkten schützen soll.

Wir sehen, dass 1 von 100 medikamentös Behandelten einen Herzinfarkt hatte (Absolutes Risiko1 = 0,01 = 1%), während insgesamt 2 von 100 Unbehandelten einen Herzinfarkt erleiden (Absolutes Risiko2 = 0,02 = 2%). Das relative Risiko (RR) beträgt rein rechnerisch RR = 1% ÷ 2% = 0,5. Das bedeutet, das Risiko für einen Herzinfarkt wird durch das Medikament um 50 % gesenkt, also halbiert!
Ist das Glas halb voll oder halb leer? Es ist relativ voll!
Diese erst einmal ziemlich imposante Aussage zur Wirksamkeit ist der Grund, warum Arzneimittelhersteller, Presseabteilungen oder Medien gern relative Risiken (oder genauer gesagt eine relative Risikoreduktion) nutzen, wenn sie nach möglichst eindrücklichen Zahlen suchen. Denn wenn wir uns das absolute Risiko für einen Herzinfarkt ansehen, so sinkt dieses durch das Medikament von 2% auf 1 %, also um gerade mal 1 Prozentpunkt. Mathematisch spricht man hier von der absoluten Risikoreduktion (ARR): ARR = 2% – 1 % = 1 %. Sie klingt häufig deutlich weniger spektakulär als eine relative Risikoreduktion.
Eine weitere Möglichkeit, eine Risikoänderung zu beschreiben
Eine andere, aus dem ARR abgeleitete Kennzahl, die helfen kann, eine Risikoänderung fassbarer zu machen und die einem auch oft in Cochrane Reviews begegnet, ist die Number needed to treat (NNT). Sie drückt aus, wie viele Personen behandelt werden müssen, damit eine von ihnen tatsächlich einen Nutzen davon hat. In unserem Beispiel liegt das auf der Hand: NNT = 100 Personen. Es müssten 100 Menschen das Medikament über den in der Studie untersuchten Zeitraum anwenden, damit ein Herzinfarkt weniger auftritt. In der Praxis gilt es dann immer abzuwägen, ob dieser Nutzen es wert ist, 99 andere Menschen den Nebenwirkungen des Medikaments auszusetzen.
Auf das Grundrisiko kommt es an!
Die Größenordnung der absoluten Risikoreduktion hängt dabei maßgeblich vom Grundrisiko des jeweiligen Ereignisses ab. Das wird durch die drei Szenarien mit unterschiedlichen Grundrisiken deutlich, inklusive unseres Beispiels in der rechten Spalte:
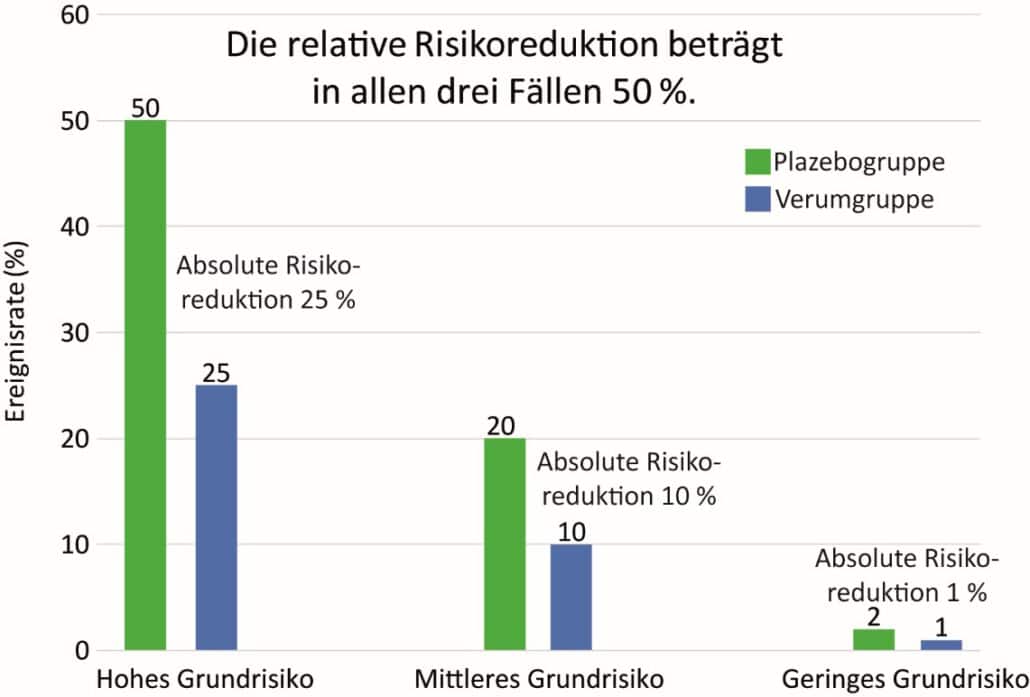
Je kleiner also das Grundrisiko (in der Placebo-Gruppe), desto stärker weichen RR und ARR voneinander ab!
Wir lernen: Vorsicht mit der Einheit Prozent [%]
Das nächste Mal, wenn Euch eine ungewöhnlich beeindruckende relatives Risikoveränderung unterkommt, schaut auch auf das absolute Risiko. Diese erlaubt oft viel besser, die wahre Größenordnung eines Problems einzuschätzen. Denn insbesondere wenn (wie bei den Haiangriffen) die absoluten Risiken niedrig sind, verleitet das in seinem Zahlenwert oft beeindruckende relative Risiko zu Fehlschlüssen. Derart vorbereitet braucht man dann auch nicht mehr seinen Urlaub am Meer abzusagen, wenn man irgendwo liest, dass sich die Zahl der tödlichen Haiangriffe von 2019 auf 2020 sogar sage und schreibe verfünffacht hat – rechnen Sie einfach selber mal nach!
Alle bisher in dieser Serie erschienenen Beiträge:
Text: Dr. Birgit Schindler



